Introdução ao Método dos Elementos Finitos: Guia Completo para Iniciantes

VirtualCAE
22/09/2023
Blog
Método dos Elementos Finitos, Simulação Virtual
0 Comentários

O Método dos Elementos Finitos (MEF) é uma técnica de simulação computacional poderosa e versátil, amplamente utilizada na análise e resolução de problemas de engenharia e ciências aplicadas, onde não é possível obter soluções analíticas exatas.

Além de ser altamente difundida no mercado e utilizada em empresas para realizar análises e melhorar a qualidade dos produtos e projetos.

Se você é um iniciante em engenharia, física ou qualquer área que lide com simulações numéricas, este guia completo o ajudará a compreender os princípios básicos do MEF e como aplicá-lo em diversas situações.

O que é o Método dos Elementos Finitos?

O MEF é uma abordagem numérica para resolver equações diferenciais parciais que descrevem o comportamento de sistemas físicos complexos. O MEF permite que esses problemas sejam discretizados em elementos finitos e aproximados por funções polinomiais, tornando a solução numérica possível . O método propõe que o número infinito de variáveis desconhecidas, sejam substituídas por um número limitado de elementos de comportamento bem definido.

Ele divide uma região ou objeto em pequenos elementos finitos, como triângulos ou quadriláteros (no caso de problemas bidimensionais) ou tetraedros e hexaedros (para problemas tridimensionais).

Cada elemento é descrito por equações matemáticas simples que representam seu comportamento local.

A divisão da geometria em pequenos elementos permite resolver um problema complexo, subdividindo-o em problemas mais simples, o que possibilita ao computador realizar com eficiência estas tarefas. A precisão do Método dos Elementos Finitos depende da quantidade de nós e elementos, do tamanho e dos tipos de elementos da malha. Ou seja, quanto menor for o tamanho e maior for o número deles em uma determinada malha, maior a precisão nos resultados da análise.

Vantagens do MEF:

Versatilidade: O MEF pode ser aplicado a uma ampla gama de problemas em diversas áreas, desde a mecânica estrutural até a simulação de processos físicos e químicos.

Precisão Ajustável: A precisão da análise pode ser controlada ajustando-se o tamanho dos elementos e o grau das funções de interpolação.

Economia de Recursos: O MEF permite simular o comportamento de estruturas e sistemas complexos sem a necessidade de protótipos físicos, economizando tempo e recursos.

Princípios Básicos do Método dos Elementos Finitos:

Geometria

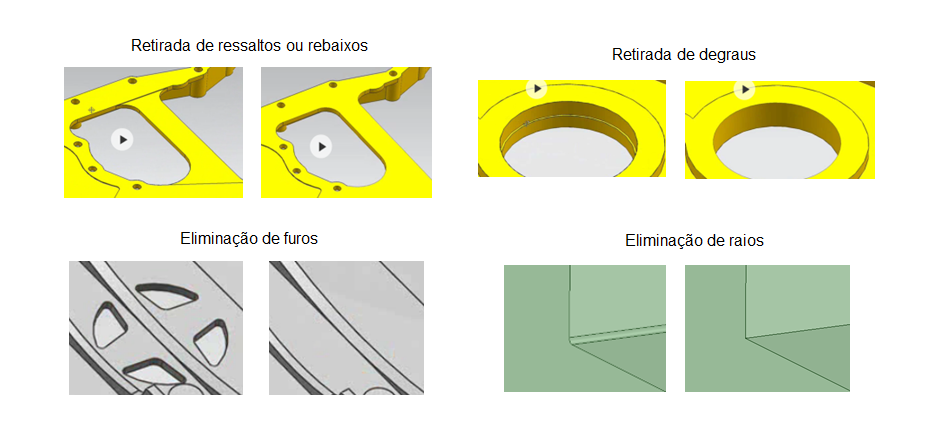
Uma parte crucial da aplicação do Método dos Elementos Finitos é a representação precisa da geometria do problema. No entanto, muitas vezes, a geometria real pode ser complexa demais para ser modelada diretamente. Nesses casos, é comum realizar uma simplificação geométrica, onde a forma real é aproximada por geometrias mais simples, como retângulos, cilindros ou esferas.

Essa simplificação permite uma análise mais acessível e eficiente, embora a precisão possa ser comprometida em certos cenários.

Material

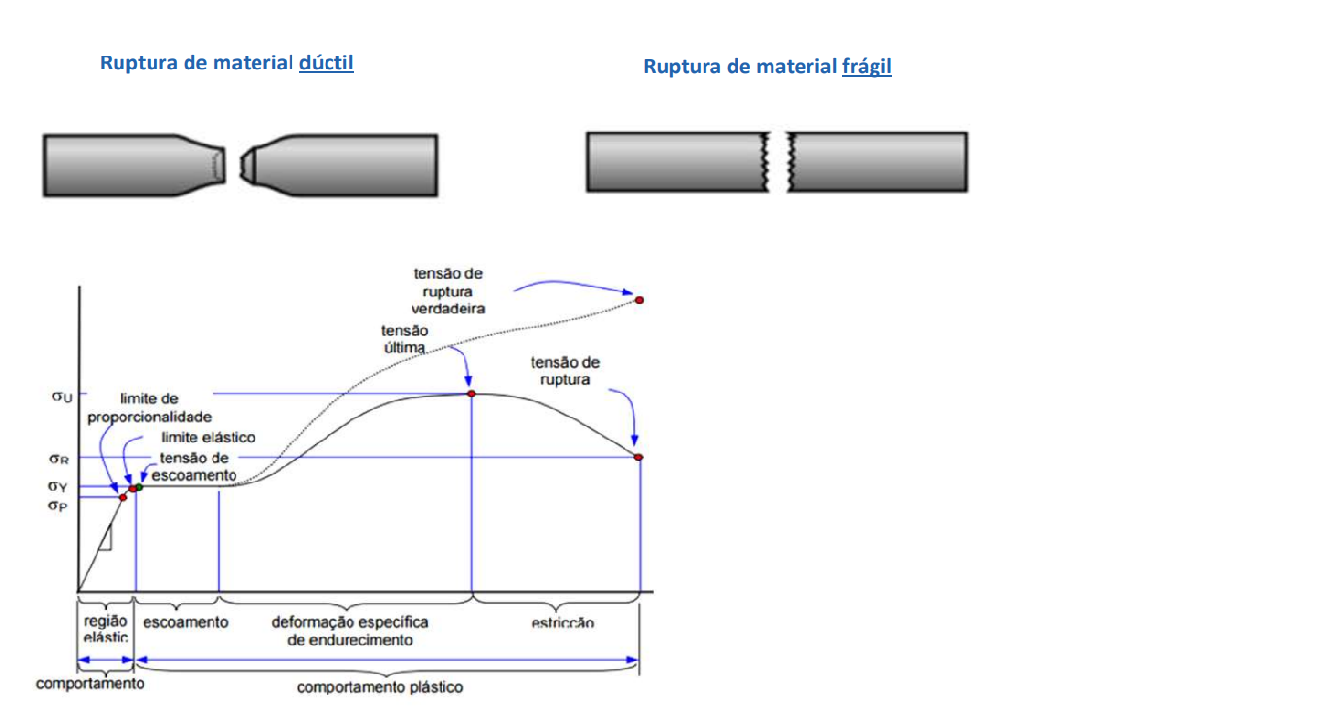
Os materiais desempenham um papel fundamental na análise de elementos finitos, pois suas propriedades afetam diretamente o comportamento do sistema. O MEF suporta uma ampla variedade de materiais, desde metais até polímeros e materiais hiperelásticos, como borrachas. Cada material é caracterizado por propriedades específicas, como módulo de elasticidade, coeficiente de Poisson, resistência à tração e outras, que são utilizadas nas equações que descrevem o comportamento do material sob carga.

Malha de Elementos Finitos

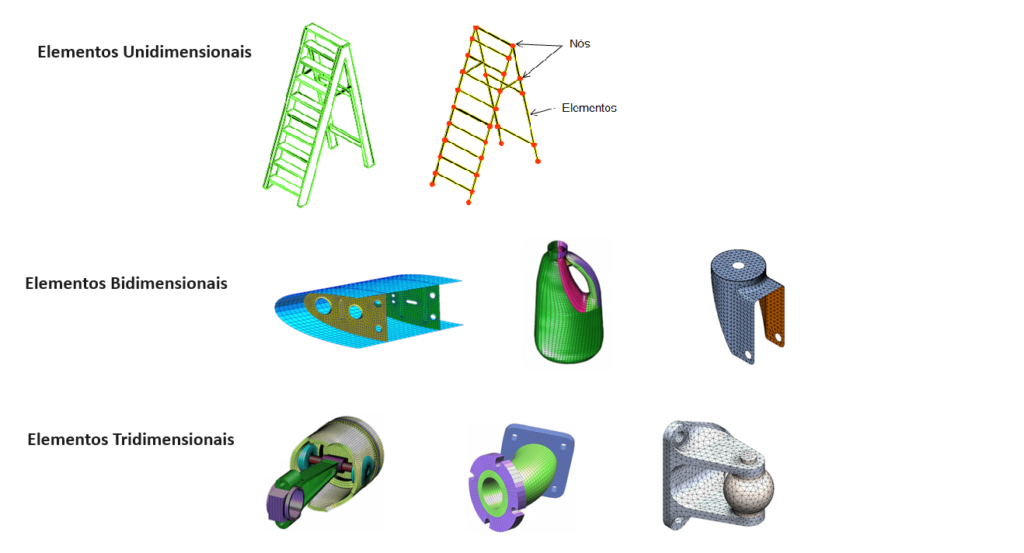
Divida a região de interesse em elementos finitos. Quanto menor o elemento, mais precisa será a análise, mas também mais computacionalmente intensiva.

A escolha da malha de elementos finitos depende da natureza do problema. Para estruturas bidimensionais, elementos de casca podem ser apropriados, enquanto problemas tridimensionais podem exigir elementos sólidos. Elementos de viga e barra são frequentemente utilizados em análises estruturais simplificadas. Cada tipo de elemento possui características específicas que se adequam às condições do problema, como restrições de deformação ou restrições de movimento.

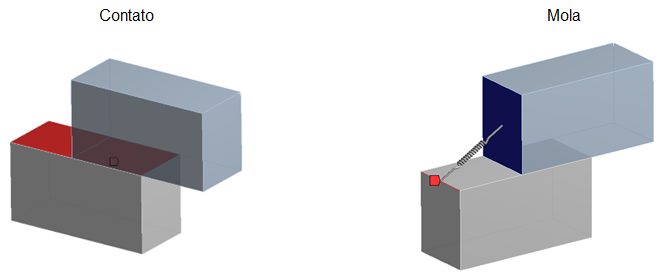
Conexões

Em sistemas complexos, a interação entre partes é frequentemente uma consideração crítica. O MEF permite a modelagem de diferentes tipos de conexões, como contatos com e sem atrito, juntas e molas. Essas conexões são essenciais para capturar o comportamento realista de montagens mecânicas, sistemas multiparte e análises de acoplamento.

Carregamentos

Aplique as condições de contorno que descrevem como o sistema se comporta nas bordas ou em pontos específicos. Isso pode incluir temperaturas fixas, forças aplicadas, deslocamentos prescritos, etc.

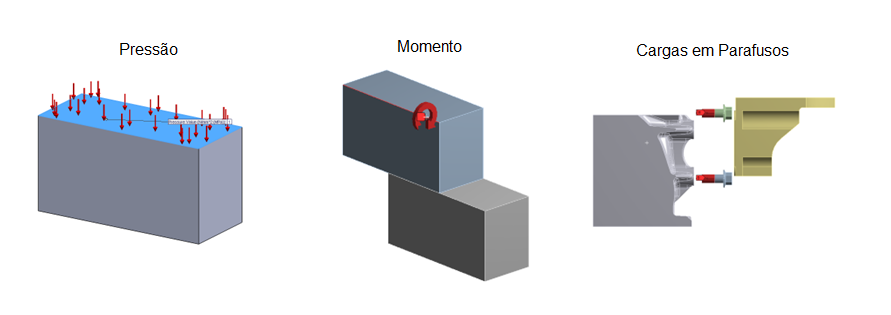
Os carregamentos aplicados a um sistema podem ser variados e incluem forças, pressões, acelerações, cargas de parafuso (pré-tensão), momentos e cargas térmicas. Além disso, é possível definir deslocamentos prescritos para representar fixações ou apoios.

A escolha adequada e a modelagem precisa desses carregamentos são cruciais para a precisão da análise.

Restrições

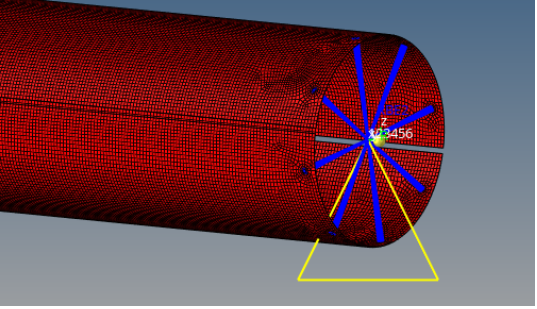
Restrições são condições que impedem o movimento de partes do sistema. Eles incluem apoios, que permitem rotação, mas não deslocamento translacional, e engastes, que impedem tanto a rotação quanto o deslocamento. A escolha e a aplicação corretas dessas restrições garantem uma representação precisa das condições de contorno do problema.

Análise

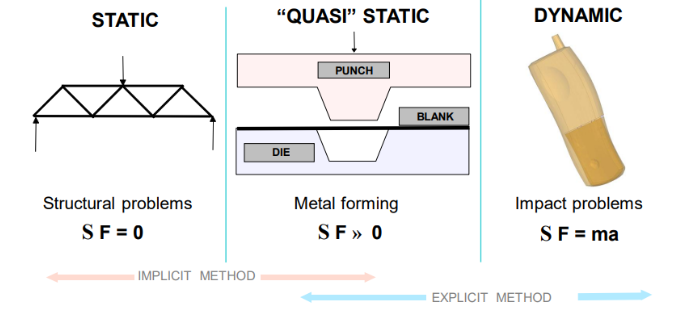
O MEF oferece uma ampla gama de tipos de análises para atender a diferentes cenários. Isso inclui análises estáticas lineares e não-lineares, análises dinâmicas como modal, resposta em frequência, análise do espectro de densidade de potência (PSD) e análise transiente. Além disso, análises termo-estruturais combinam análises térmicas e estruturais para problemas acoplados. A análise de fadiga permite avaliar a vida útil do componente em condições cíclicas de carregamento.

Resultados

Os resultados da análise de elementos finitos são essenciais para a tomada de decisões de engenharia. Isso inclui informações sobre deslocamentos, tensões (que podem ser avaliadas quanto a limites de tensão), vida e dano em fadiga (para prever a durabilidade do componente) e fator de segurança (para garantir a segurança do projeto).

Analise os resultados obtidos e visualize-os para obter informações úteis sobre o problema.

Gráficos, contornos e animações podem ser gerados para facilitar a interpretação dos resultados.

O Método dos Elementos Finitos é uma ferramenta poderosa que revolucionou a forma como engenheiros e cientistas abordam problemas complexos.

À medida que você ganha experiência, poderá aplicar esses princípios a problemas cada vez mais desafiadores e explorar as inúmeras aplicações que o MEF oferece.

A VirtualCAE oferece material completo e exclusivo para seus estudos na área de Engenharia.

Conheça clicando aqui!

Tags: Método dos Elementos Finitos Simulação Virtual